When precreasing a crease pattern, we always need to start somewhere. The points in the crease pattern, that can be used to construct the rest of it are called reference points. Therefore every precrease starts with getting them, with finding a reference. For Boxpleating and Hexpleating the “reference points” are the grid.
Finding these points without help can be quite difficult. Luckily there is a Reference Finder online that has been published by Mu Tsun Tsai.
Additionally, I stumbled upon a system that can be used to find fractions. It is relatively easy and leads to precise results which is why I still use it to find most grids. It works as follows:
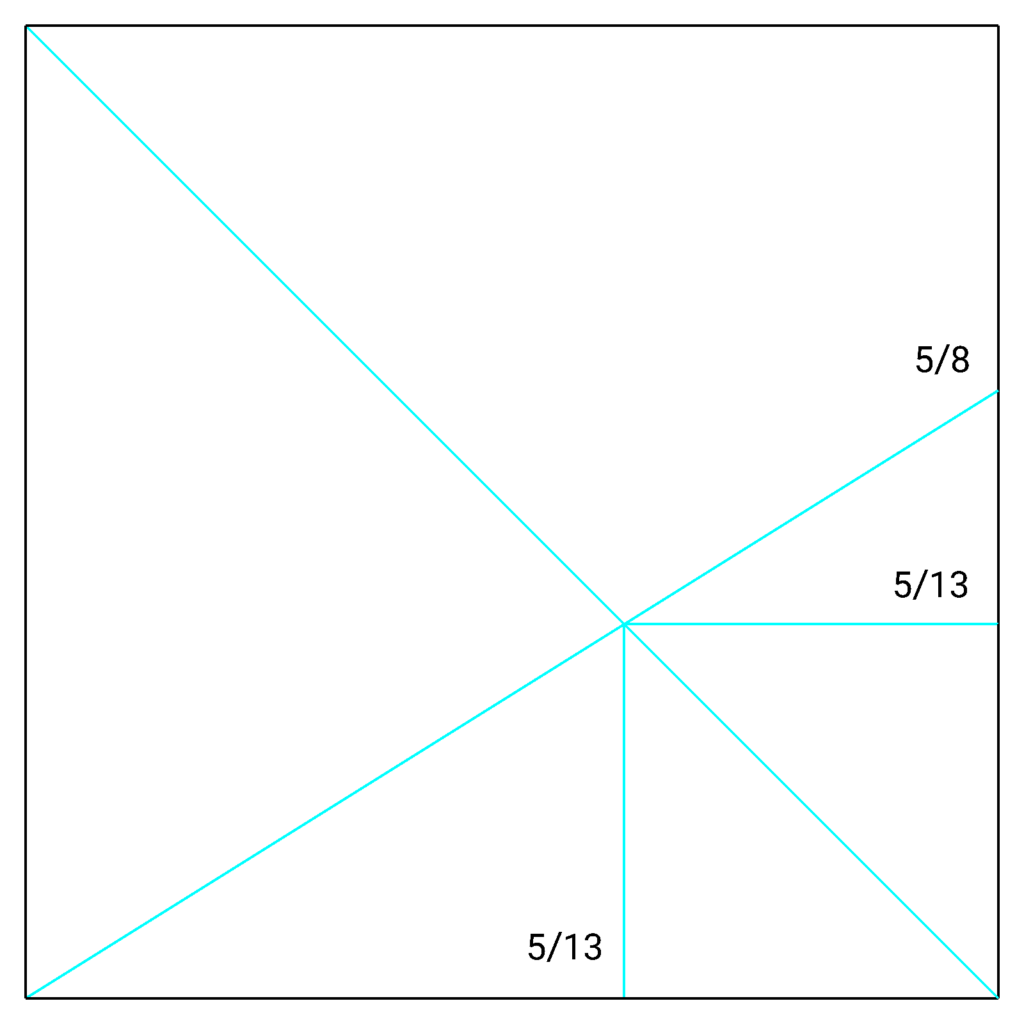
Instructions for finding a reference
First of all, you need to decide, in how many divisions shall be made. The number of equal divisions will be called N. N= {3; 4; 5; 6; ….}
For example in a 13 x 13 grid there are 13 equal divisions and N= 13.
Next we need to find the highest power of 2 that fits into n.
It the condition N/2 < 2n < N can be applied for that; n= {0; 1; 2; 3; … }
For a 13 x 13 grid 2n = 23 because 23 = 8 and 6.5 < 8 < 13
Third, we subtract 2n from N. I will call the result k; k = {1; 2; 3; 4; … }
In our example, N – 2n = k; k= 13- 8= 5
Now, we make a pinch mark on the right sight of the square and make a pinch at k/ 2n (counting from the bottom).
In our example, that´s 5/8.
One can make this pinch easily by folding, because dividing a side in 2, 4 or 8 divisions works without further reference.
Next, we connect the mark k/ 2n on the right side with the bottom left corner. Additionally, we crease the diagonal running from the top left to the bottom right corner.
Of course, you can also use pinches here, we just need to find the intersection of these lines.
For the intersection is a point on the desired grid eg. the inersection marks the point 5/13 of the diagonal.
I use this method quite often and I can recommend it for 3rds, 5ths, 7ths, 11ths…
However for finding 9ths or 17ths, I recommend using a different method. Not because it wouldn`t work, but due to the fact that the reference lines for them are painful to fold precisely.
Why does that system work?
The bottom left corner of the square is given the coordinates (0/0),
The bottom right corner is (0/1)
The top left corner is (0/1)
The top right corner of the square is (1/1)
Therefore the pinch mark we construct has the coordinates ( 1/ (k/ 2n )) and
the line connecting the mark and the bottom left corner is the line y= k/ 2n * x.
The diagonal from the top left to the bottom right corner is y= 1- x
For the intersection, I calculated
k/ 2n * x = 1-x
x = 2n/ k – 2n/k*x
(1+ 2n/k)*x = 2n/k
x = ( 2n/ k) / (1-+ 2n/ k)
x = 2n / (k+2n ) since N = k +2n
Therefore x= 2n/N and y= k/N.
That´s why this method is applicable for finding a reference for every grid with N equal divisions.
